В прошлой статье мы разбирались,что такое бенчмаркинг кода и как с его помощью оценивать производительность кода. В этой же поговорим про оценку сложности алгоритмов. А чтобы всё было наглядно, вместе попробуем оценить алгоритмы, которые используются для решения задачки на собеседовании в Google.
Задач такого плана полным-полно на платформах типа LeetCode, CodeWars и других. И их ценность не в том, чтоб заучить различные алгоритмы сортировок, которые вы никогда не будете на практике писать самостоятельно, а в том, чтоб увидеть типичные проблемы, с которыми вы можете столкнуться в практических задачах при разработке.
Оценка сложности алгоритмов
Зачем вообще оценивать сложность алгоритмов и какие способы оценки бывают?
Понимать сложность алгоритмов важно и по следующим причинам:
- без этих знаний вы не сможете отличить суб-оптимальный код от оптимального и оптимизировать его;
- каждый средний или большой проект рано или поздно будет оперировать большим объёмом данных. Важно, чтоб ваши алгоритмы это предусматривали и не стали бомбой замедленного действия;
- если вы не понимаете концепции оценки сложности алгоритмов, вы, скорее всего, будете писать низкопроизводительный код по умолчанию.
Способы же оценки сложности существуют следующие:
O большое (O(n)) — позволяет оценить верхнюю границу сложности алгоритмов. Это отношение количества входных данных для алгоритма ко времени, за которое алгоритм сможет их обработать. Простыми словами, это максимальное время работы алгоритма при работе с большими объёмами данных.
o малое (o(n)) — позволяет оценить верхнюю границу, исключая точную оценку.
Омега (Ω(n)) — позволяет оценить нижнюю границу сложности.
Тета (Θ ()) — позволяет получить точную оценку сложности.
В большинстве IT-компаний для оценки сложности используют только большое O (BigO notation), поскольку чаще всего достаточно представлять, как быстро будет расти количество операций при увеличении входных данных в худшем случае. Остальные типы оценок используются редко.
Если представить график распространённых сложностей алгоритмов, они будут выглядеть вот так:
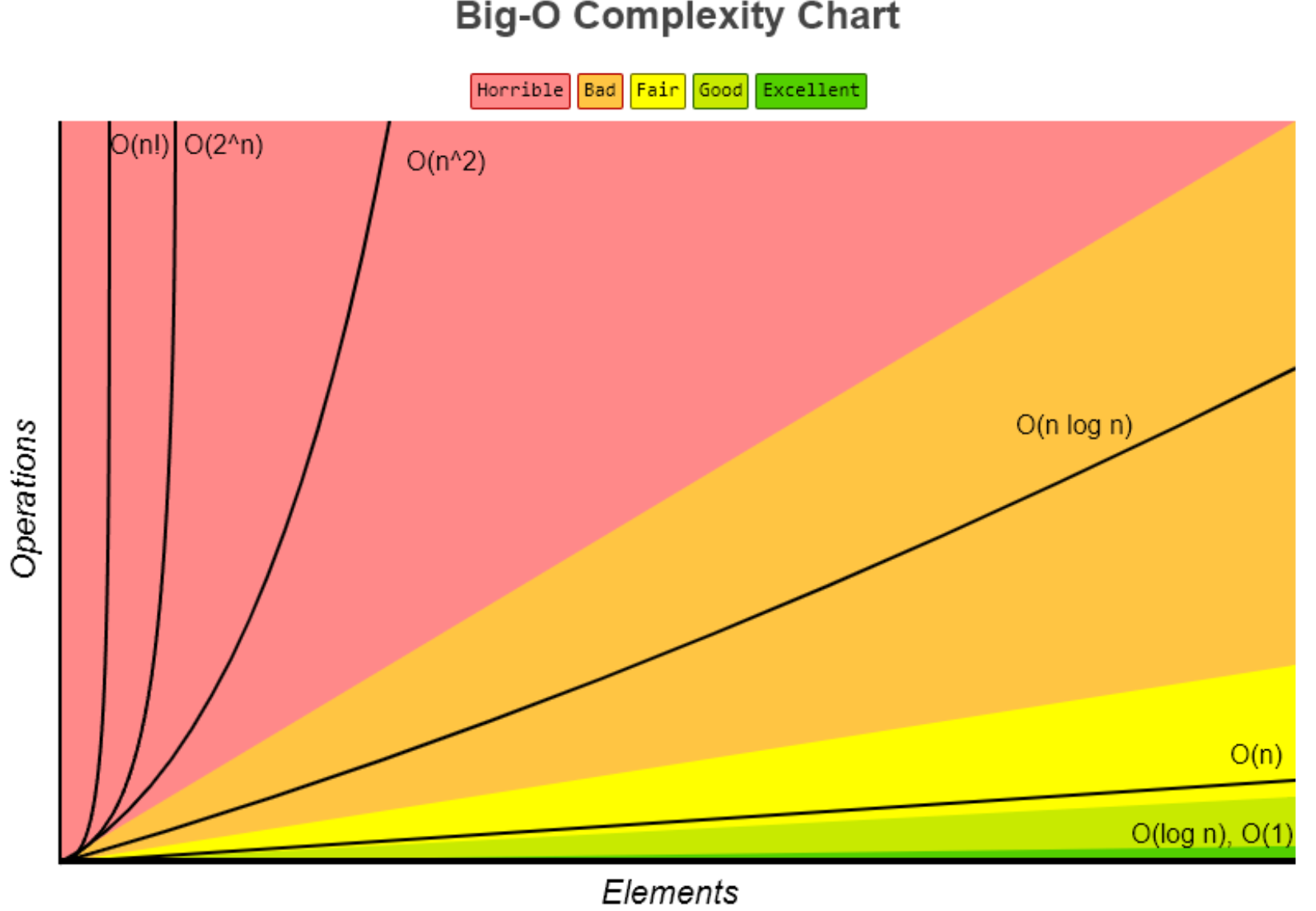
Если условно разделить сложности на зоны, то сложности вида O(log n), O(1) или O(C) можно будет отнести к зоне Excellent. Такие алгоритмы вне зависимости от объёмов данных будут выполняться очень быстро — практически мгновенно.
Алгоритмы сложности O(n) можно отнести к зоне Fair — к алгоритмам, сложность которых растёт предсказуемо и линейно. Например, если 100 элементов ваш алгоритм обрабатывает за 10 секунд, то 1000 он обработает примерно за 100 секунд. Не лучший результат, но предсказуемый.
Алгоритмы из красной зоны Horrible со сложностями O(N^2) и выше трудно отнести к высокопроизводительным. НО! Тут всё сильно зависит от объёмов входных данных. Если вы уверены, что у вас всегда будет небольшой объём данных (например, 100 элементов), и обрабатываться он будет в приемлемое для вас время, то всё в порядке, такие алгоритмы тоже можно использовать. Но если же вы не уверены в постоянности объёмов данных (может прийти и 10 000 элементов вместо 100) — лучше всё-таки задуматься над оптимизацией алгоритмов.
Оценка сложности по времени и по памяти
Оценку сложности алгоритмов следует проводить не только по времени выполнения, но и по потребляемой памяти. Например, для ускорения вычислений можно создать какую-нибудь промежуточную структуру данных типа массива или стека для ускорения алгоритма и кеширования результатов. Это приведёт к дополнительным затратам памяти, но при этом может существенно ускорить вычисления.
Однако если ваш алгоритм для выполнения будет требовать больше памяти, чем может предоставить ваш ПК, вы не получите ожидаемой производительности. А возможно код и вовсе будет выполнен некорректно.
Немного практики:правила расчета сложности
Пример 1:
Возьмём для начала простой алгоритм присвоения переменной:
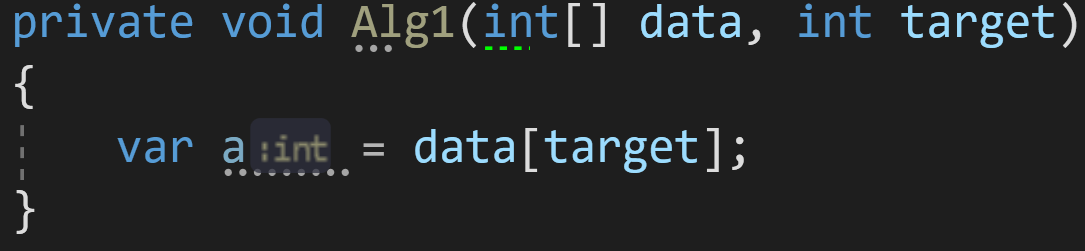
Какова его сложность по времени и по памяти?
С одной стороны, нас может ввести в заблуждение массив данных data неизвестной размерности. Но брать его в расчёт при оценке сложности внутреннего алгоритма будет некорректно.
Получается, наш алгоритм состоит только из одной строчки: var a = data[target];
Доступ к элементу массива по индексу — известная операция со сложностью O(1) или O(C). Соответственно, и весь алгоритм по времени у нас займет O(1).
Дополнительная же память выделяется только под одну переменную. А значит, объём данных, которые мы будем передавать (хоть 1 000, хоть 10 000), не скажется на финальном результате. Соответственно, сложность по памяти у нас так же — O(1) или O(C).
Пример 2:
Рассмотрим второй алгоритм, очень похожий на первый:
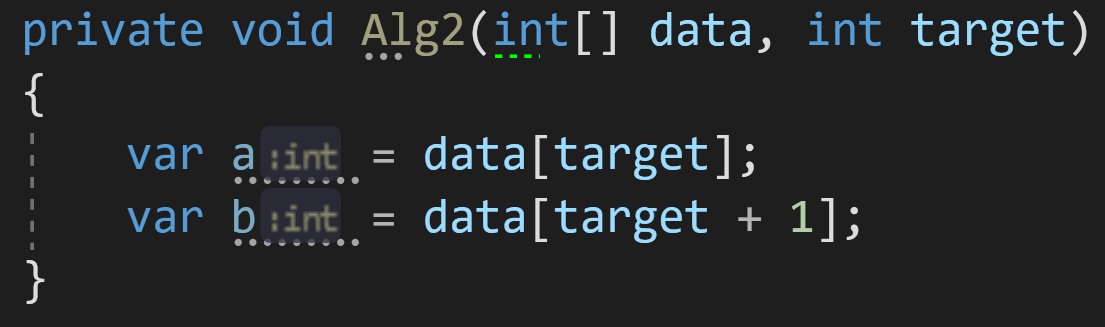
Влияет ли размерность входного массива data на количество операций в нём? Нет.
А на выделенную память? Тоже нет.
Сложность этого алгоритма по времени выполнения можно было бы оценить как O(2*C) — поскольку у нас выполняется в два раза больше операций, чем в предыдущем примере, 2 присваивания вместо 1. Но у нас и на этот счёт есть правило:
Если принять это правило в расчёт, сложность этого алгоритма будет такой же, как и в первом примере — O(C) по времени и O(C) по памяти.
Пример 3:
В третьем примере добавим в наш алгоритм цикл для обработки данных:
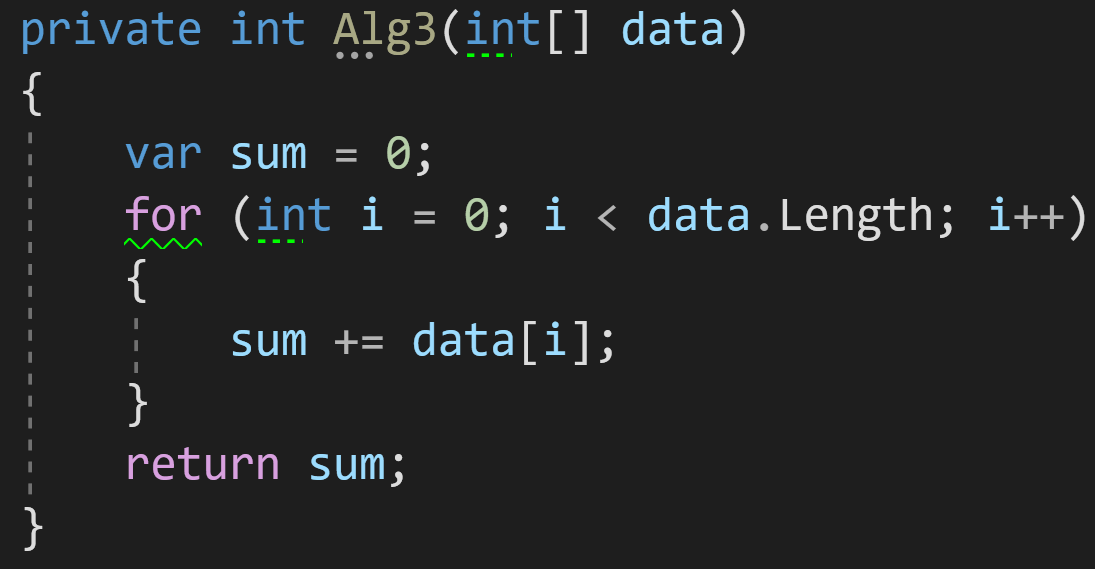
Как мы видим, количество операций, которые будет выполнять цикл, напрямую зависит от количества входных данных: больше элементов в data — больше циклов обработки потребуется для получения финального результата.
Казалось бы, если взять в учёт каждую строчку кода нашего алгоритма, то получилось бы что‑то такое:
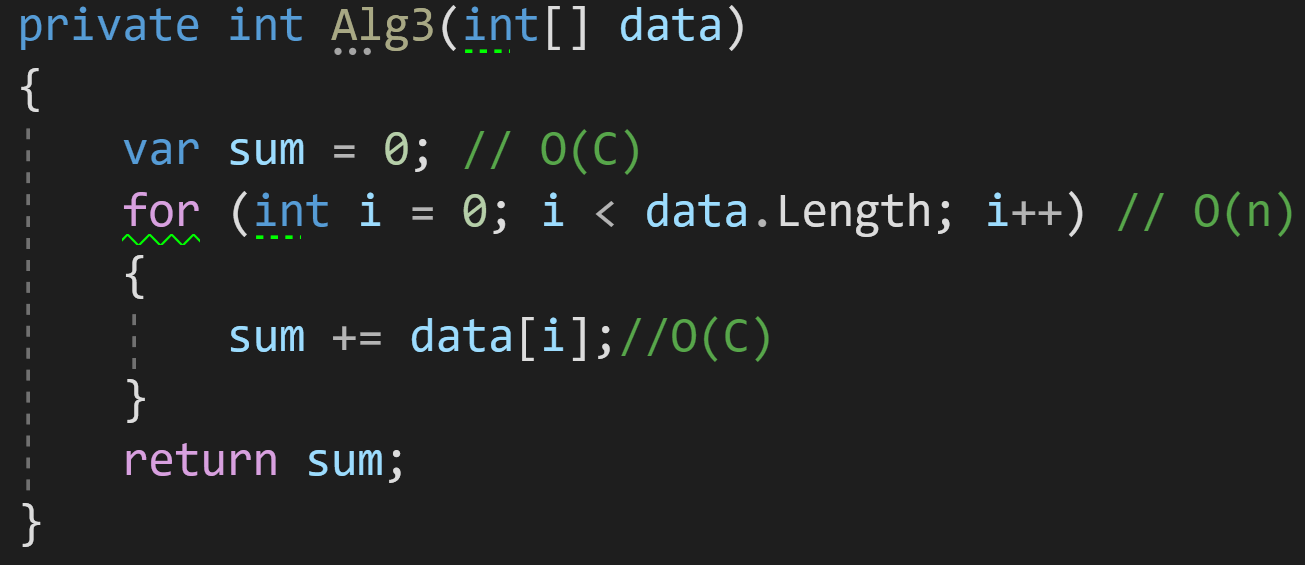
И тогда финальная сложность алгоритма получится O(C)+O(n). Но тут опять вмешивается новое правило:
Поясню: если у вас O(C)+O(n), результирующая сложность будет O(n), поскольку O(n) будет расти всегда быстрее, чем O(C).
Еще один пример — O(n)+O(n^2). При такой сложности у нас N^2 всегда растёт быстрее, чем N, а значит O(n) мы отбрасываем и остаётся только O(n^2).
Итак, сложность нашего третьего примера — O(n).
Пример 4:
В четвёртом примере добавим на вход уже двумерный массив.
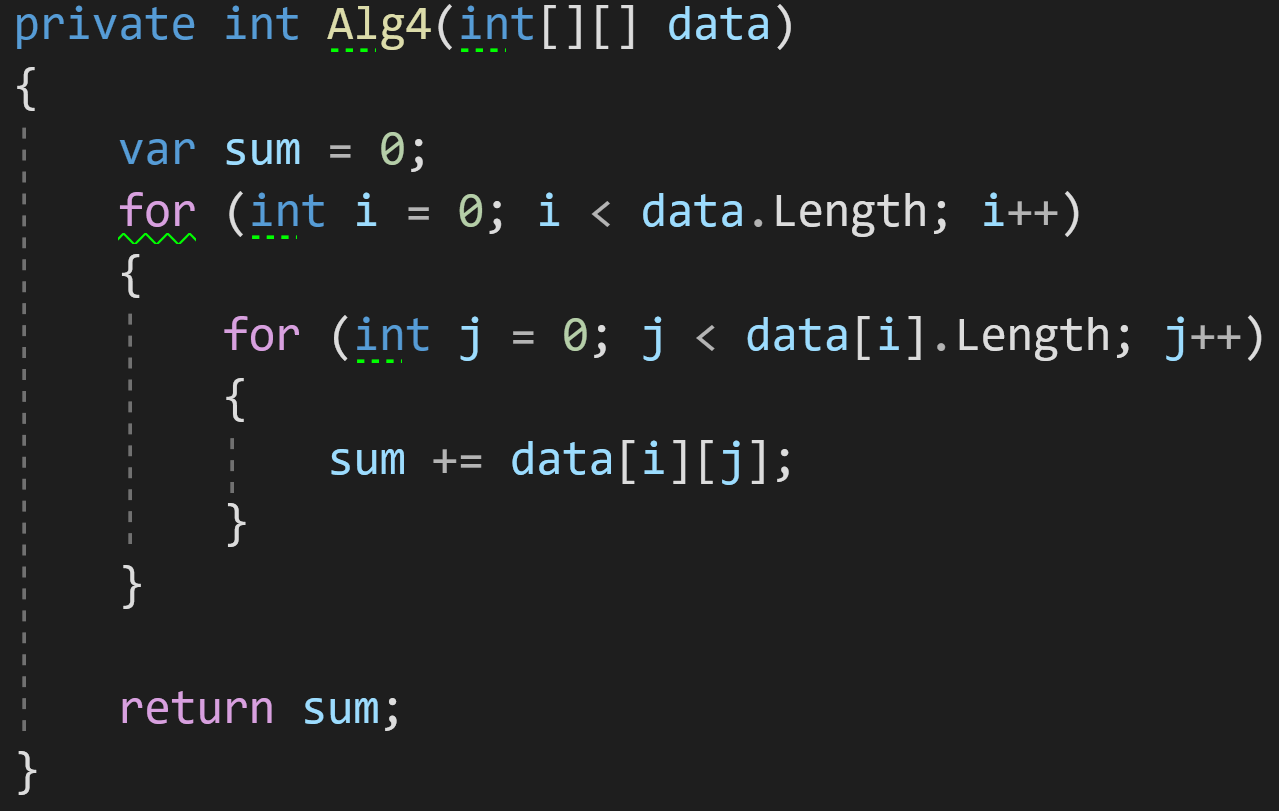
И для его обработки нам теперь нужно два цикла. Оба этих цикла будут зависеть от размерности входных данных data.
Сложность внешнего цикла в нашем примере — O(N), сложность внутреннего цикла — O(N) (или O(M), если массив не квадратный). Согласно правилу, две эти сложности должны быть умножены. В результате максимальная сложность всего алгоритма будет равна O(N^2).
Пример 5:
А что мы видим тут? Цикл — уже известная нам сложность O(n), но внутри вызывается функция Alg4() из предыдущего примера:
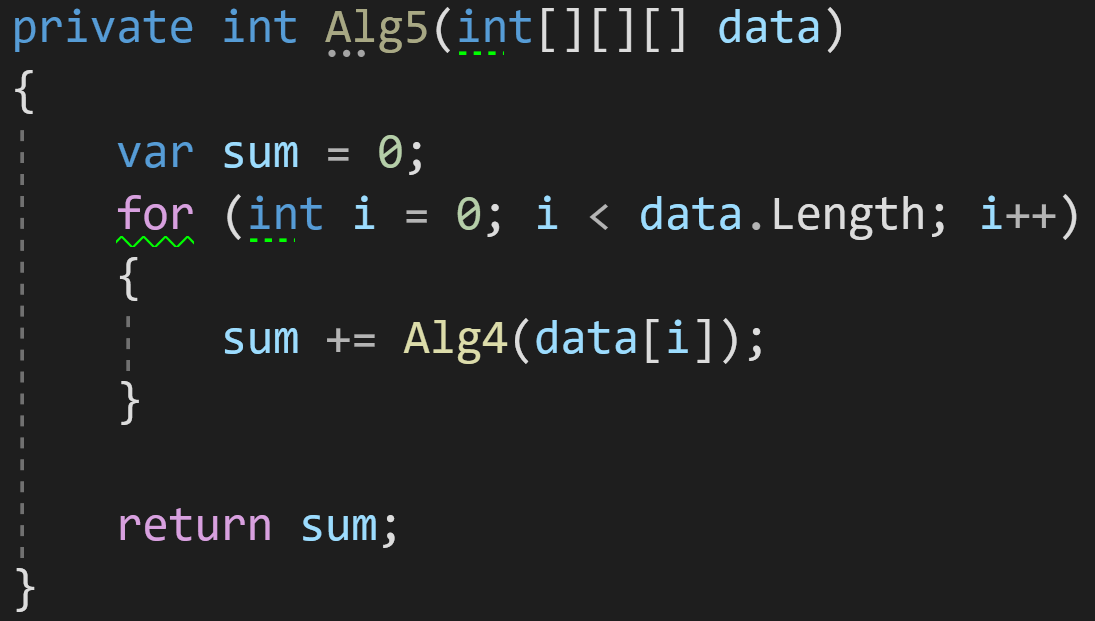
Если мы вспомним её сложность O(n^2), а также правило 4, то получим, что сложность этого алгоритма — O(n^3) при всей его визуальной минималистичности.
Именно поэтому важно понимать сложность методов синтаксического сахара вроде LINQ — чтоб была возможность оценить, как метод будет вести себя при увеличении объёмов данных. При использовании их в коде без понимания внутреннего устройства вы рискуете получить очень высокую сложность алгоритма, который будет захлебываться при увеличении входящих данных.
Приведу пример минималистичного алгоритма, который выглядит хорошо и компактно (ни в коем случае не претендует на эталонный код), но станет бомбой замедленного действия при работе с большими объёмами данных:
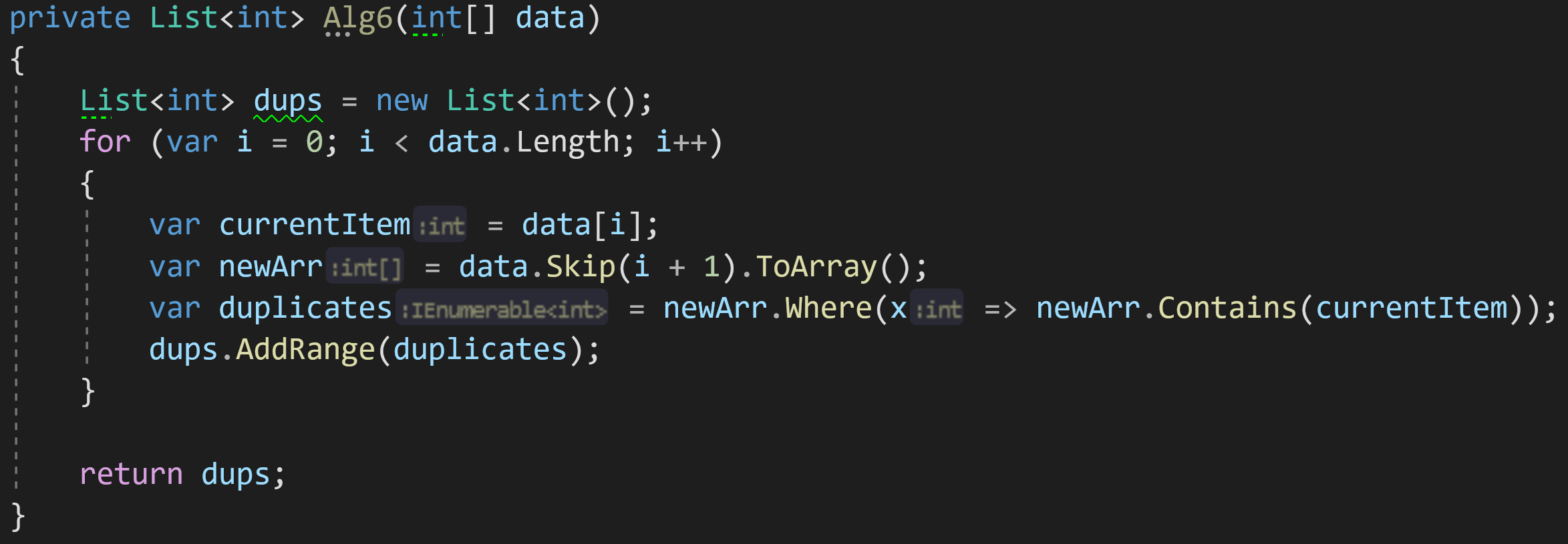
Что мы тут видим? Цикл = O(n), Where = от O(1) до O(n), в зависимости от типа хранящихся внутри данных, Contains = O(n).
Итого сложность такого алгоритма будет от O(n^2) до O(n^3) по времени выполнения.
ToArray() будет выделять на каждой итерации дополнительную память под копию массива, а значит сложность по памяти составит O(n^2).
Задачка от Google
Возьмём для нашего финального оценивания задачку, которую дают на собеседовании в Google.
Вкратце, цель алгоритма — найти в массиве два любых числа, которые в сумме дали бы нам искомое число target.
Решение 1: полный проход по массиву
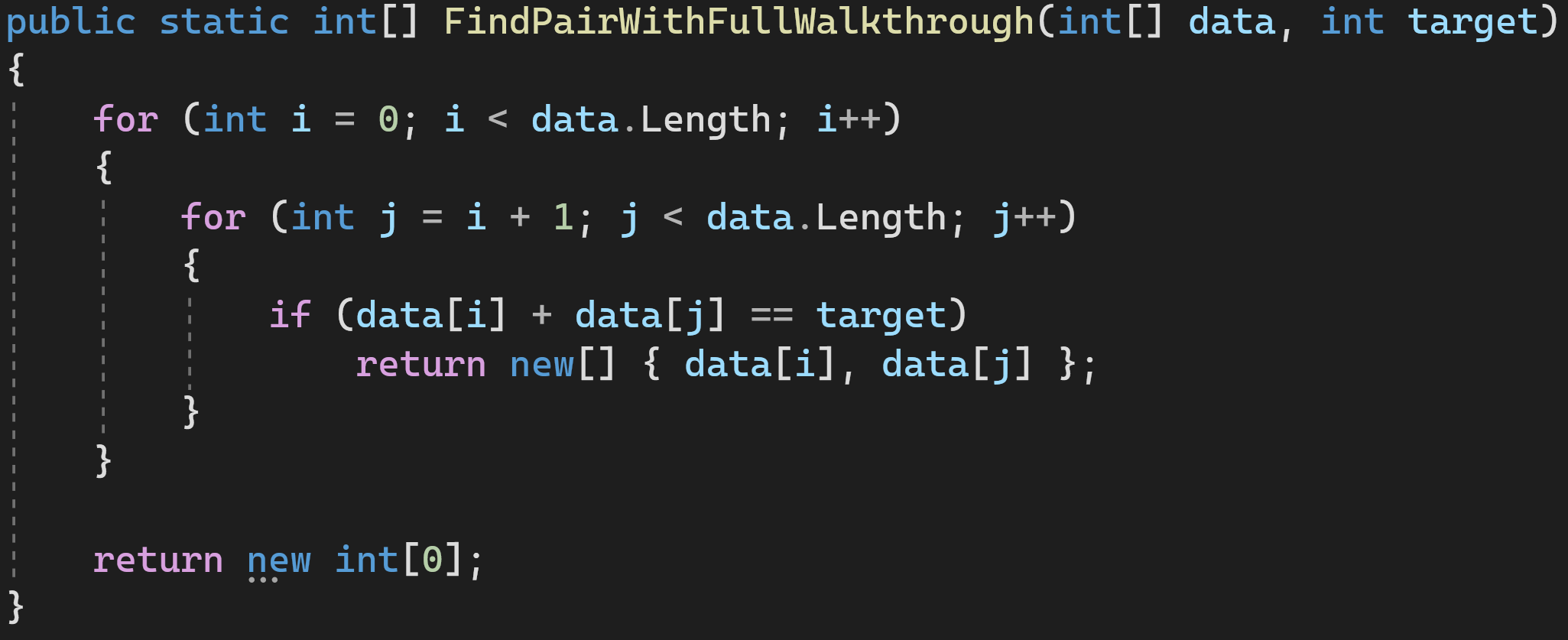
Сложность по времени: O(n^2)
Сложность по памяти: O(С)
Это решение в лоб. Не самое оптимальное, поскольку время быстро растёт при увеличении количества элементов, но зато дополнительную память мы особо не потребляем.
Решение 2: используем HashSet
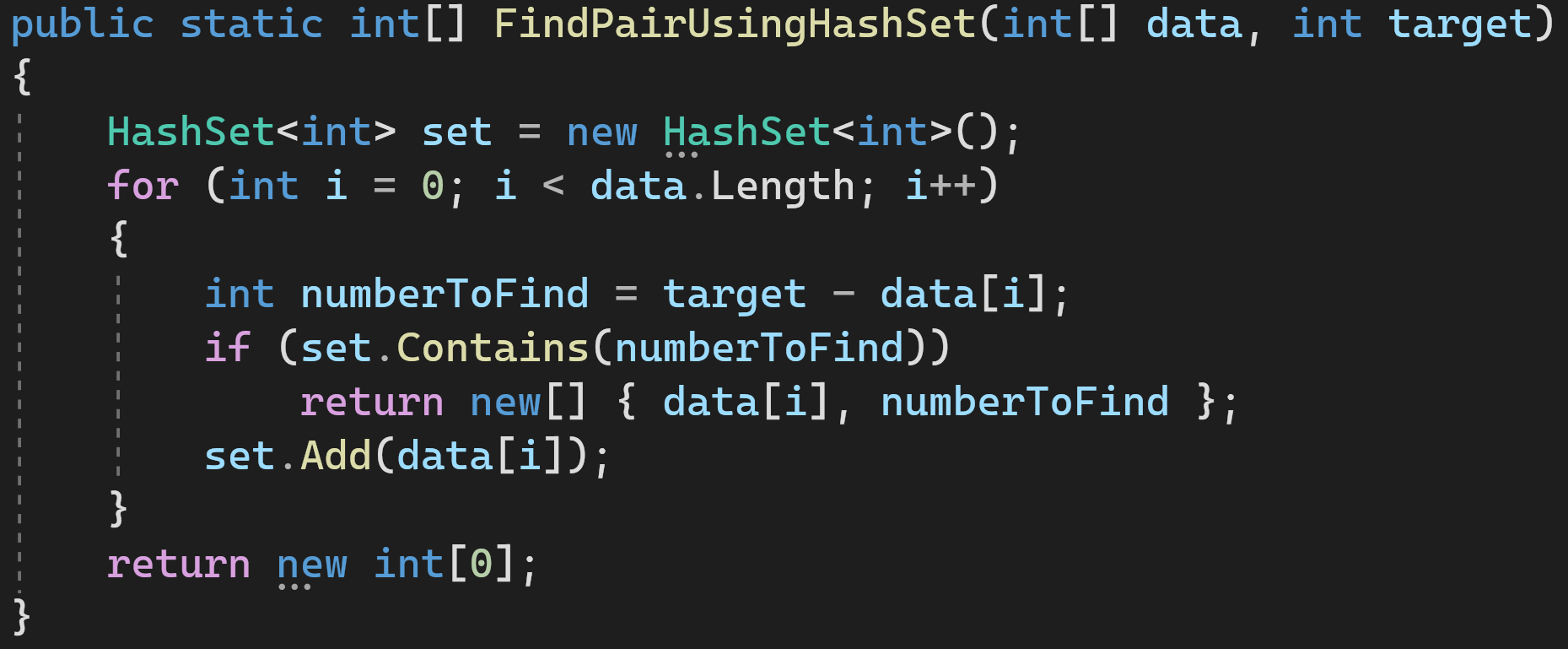
Проходимся по массиву и добавляем элементы, которые мы уже проверили, в HashSet. Если HashSet содержит недостающий для суммы элемент, значит всё хорошо, мы закончили и можем возвращать результат.
Сложность по времени: O(n)
Сложность по памяти: O(n)
Это как раз пример того, как можно выиграть в производительности, выделив дополнительную память для промежуточных структур.
Решение 3: используем бинарный поиск
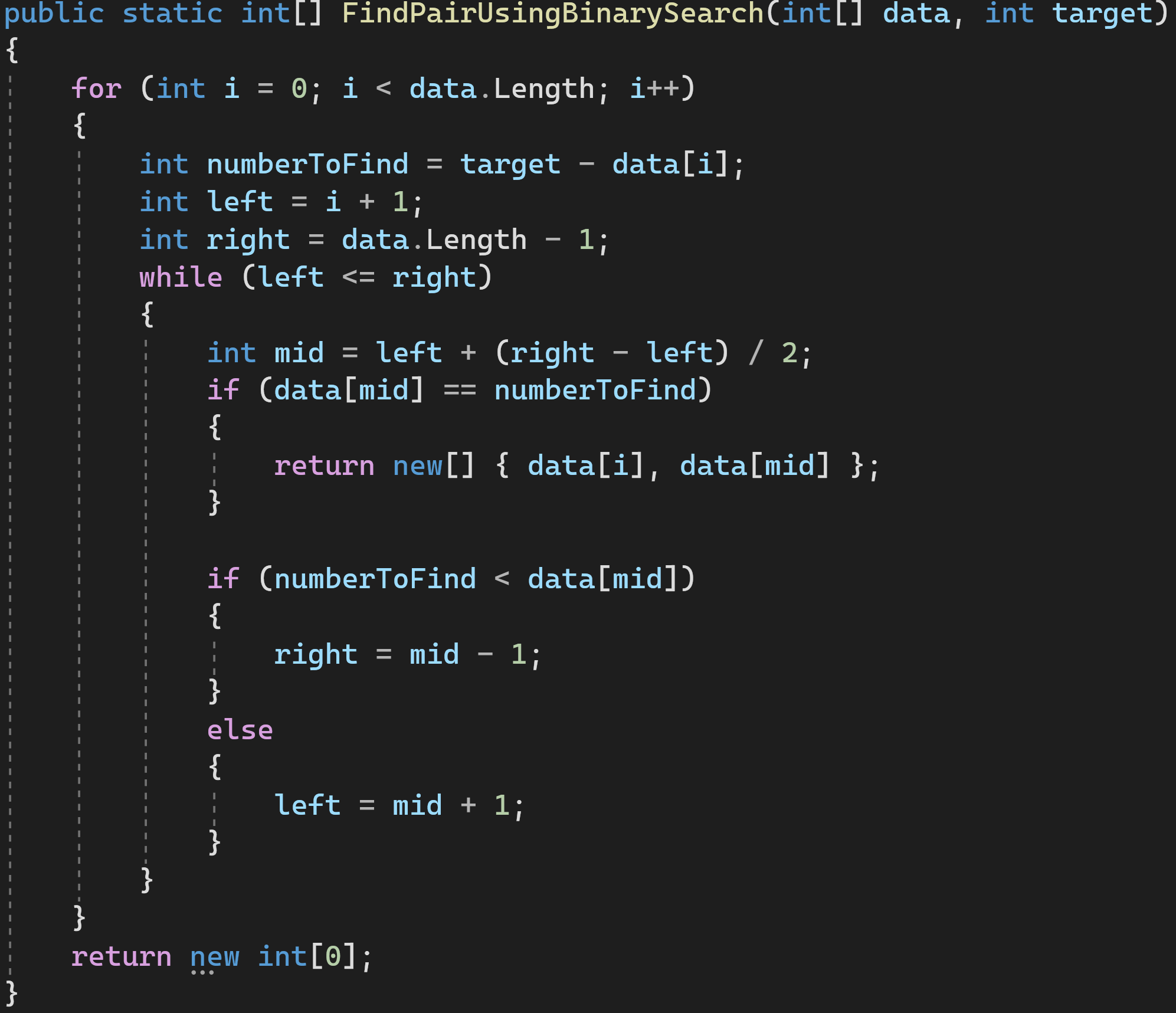
Алгоритм бинарного поиска имеет известную сложность — O(log(n)). O(n) нам добавилась от внешнего цикла for, а всё, что внутри цикла while — это и есть алгоритм бинарного поиска. Согласно Правилу 4 сложности перемножаются.
Сложность по времени: O(n*log(n))
Сложность по памяти: O(С)
Решение 4: используем метод двух указателей
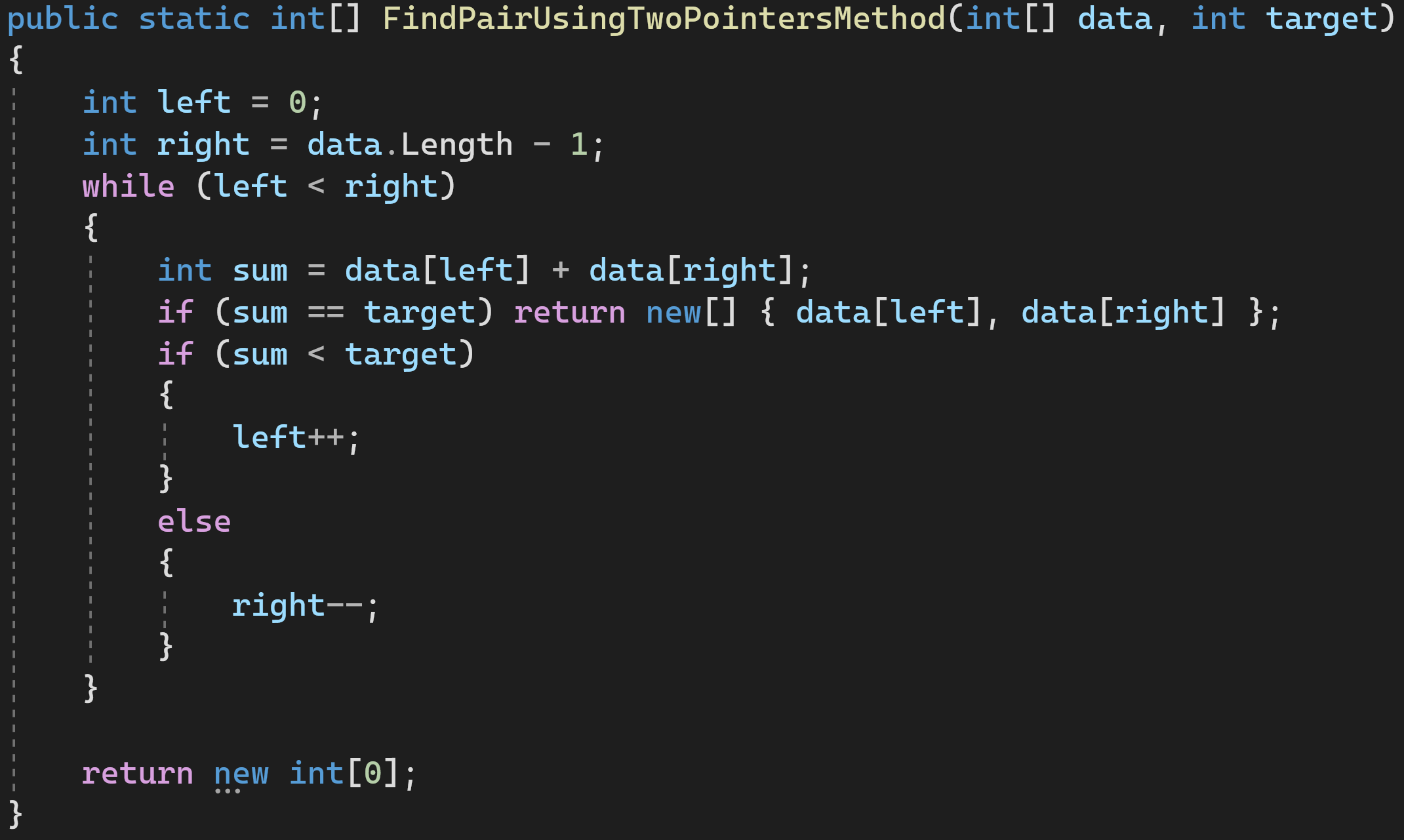
Двигаем левый и правый указатели к центру, пока они не сойдутся или не найдется пара подходящих нам значений.
Сложность по времени: O(n)
Сложность по памяти: O(С)
И это — самый оптимальный из всех вариантов решения, не использующий дополнительной памяти и совершающий наименьшее количество операций.
Бенчмаркинг решений
Теперь, зная сложности всех четырёх вариантов решения, попробуем провести бенчмаркинг этого кода и посмотреть, как алгоритмы будут вести себя на различных наборах данных.
Результаты будут следующими:
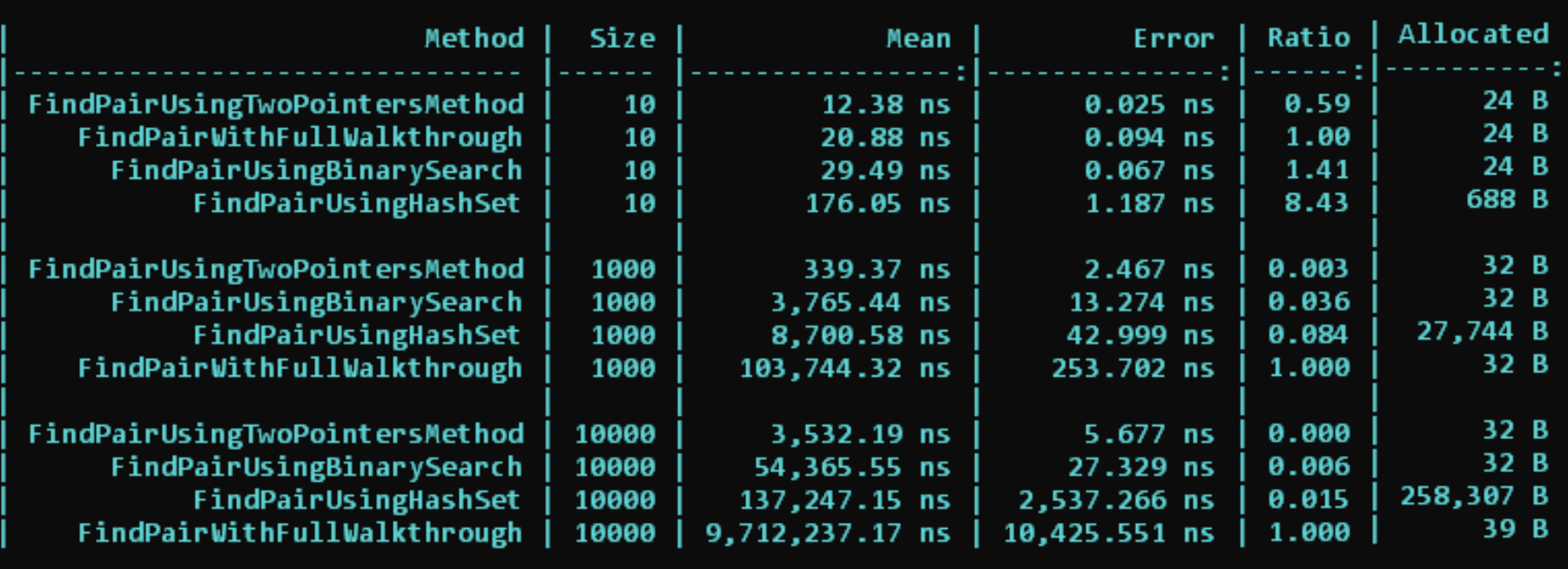
Что же мы тут видим?
За baseline решения мы берём прямой проход массиву FindPairWithFullWalkthrough. На 10 объектах он отрабатывает в среднем за 20 наносекунд и занимает второе место по производительности.
Быстрее на малом объёме данных выполняется только наш самый оптимальный вариант решения — FindPairUsingTwoPointersMethod.
Вариант же с HashSet занял в 8 раз больше времени для работы с малым объёмом данных и потребовал выделения дополнительной памяти, которую потом нужно будет собрать Garbage Collector-у.
На 1 000 же элементов вариант с полным проходом по циклу (FindPairWithFullWalkthrough) начал заметно отставать от остальных алгоритмов. Причиной этому — его сложность O(n^2), которая растёт заметно быстрее всех остальных сложностей.
На 10 000 элементах алгоритму с полным проходом потребовалось и вовсе 9,7 секунды для завершения расчетов, в то время как остальные справлялись за 0.1 секунды и меньше. А самый оптимальный вариант решения и вовсе нашёл решение за 3 миллисекунды.
Заключение
Мы разобрались, как оценивать сложность алгоритмов, а также узнали, как с помощью BenchmarkDotNet проследить связь между сложностью алгоритмов и временем выполнения кода. Это позволит нам ещё до выполнения бенчмаркинга приблизительно оценить — хороший код вы написали или нет.
Фото в заголовке: by Joshua Sortino on Unsplash
Автор: Антон Воротынцев
Редактура: Марина Медведева




